こちらもCHECK こちらもCHECK LINEST 関数を使った最小二乗法 Excelには、最小二乗法による直線式を求める関数として「LINEST 関 ... 続きを見る
最小二乗法 Excel版【関数による求め方、散布図への近似曲線と数式の表示】
最小二乗法とは
最小二乗法とは、誤差を含むデータの処理において、その誤差の二乗の和を最小にすることで最も確からしい関係式を求める方法である。
相関関係を調べる、または実験式の作成の際に用いる統計的手法の一つである。
例えば、次のデータについて考える。これらのデータには正の相関が見られるが、プロットは一直線上に並んでいない。
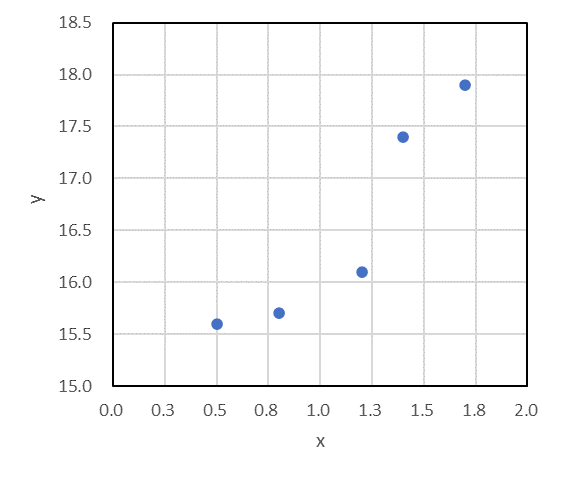
このデータが線形一次方程式の形( y = ax + b )で表されると仮定して、最も確からしい直線式を求める手法が最小二乗法だ。
最小二乗法の近似式の求め方
データが一次方程式の形( y = ax + b )で表されると仮定する。
最小二乗法により傾きと切片を求めていく。
まずデータ を求め次のようにまとめる。
| No. | x | y | x2 | xy |
| 1 | 0.5 | 15.6 | 0.25 | 7.8 |
| 2 | 0.8 | 15.7 | 0.64 | 12.56 |
| 3 | 1.2 | 16.1 | 1.44 | 19.32 |
| 4 | 1.4 | 17.4 | 1.96 | 24.36 |
| 5 | 1.7 | 17.8 | 2.89 | 30.43 |
| $\displaystyle \sum$(総和) | 5.6 | 82.7 | 7.18 | 94.47 |
| ①n | ②$\displaystyle \sum_{ i=1 }^{ n }x_{ i }$ | ③$\displaystyle \sum_{ i=1 }^{ n }y_{ i }$ | ④$\displaystyle \sum_{ i=1 }^{ n }x_{ i } \hspace{0.5pt} ^2$ | ⑤$\displaystyle \sum_{ i=1 }^{ n }x_{ i }y_{ i }$ |
※①データの個数n
このデータではn=5
次の式に当てはめてaとbを求めていく。
\begin{eqnarray} a &=& \frac{n \displaystyle \sum_{ i=1 }^{ n }x_{ i }y_{ i }-( \displaystyle \sum _{ i=1 }^{ n }x_{i})( \displaystyle \sum_{ i=1 }^{ n }y_{ i })}{n \displaystyle \sum_{ i=1 }^{ n }x_{ i } \hspace{0.5pt} ^2-( \displaystyle \sum_{ i=1 }^{ n }x_{ i })^2} \\[5pt]&=&\frac{①×⑤-②×③}{①×④-②^2} \\[5pt]
&=& \frac{5×94.47-5.6×82.7}{5×7.18-(5.6)^2} \\[5pt] &=& 2.03 \end{eqnarray}
&=& \frac{5×94.47-5.6×82.7}{5×7.18-(5.6)^2} \\[5pt] &=& 2.03 \end{eqnarray}
\begin{eqnarray}b &=& \frac{( \displaystyle \sum _{ i=1 }^{ n }x_{ i } \hspace{0.5pt} ^2)( \displaystyle \sum _{ i=1 }^{ n }y_{ i })-( \displaystyle \sum _{ i=1 }^{ n }x_{ i })( \displaystyle \sum _{ i=1 }^{ n }x_{ i }y_{ i })}{n \displaystyle \sum _{ i=1 }^{ n }x_{ i } \hspace{0.5pt} ^2-( \displaystyle \sum_{ i=1 }^{ n }x_{ i })^2} \\[5pt] &=& \frac{④×③-②×⑤}{①×④-②^2} \\[5pt] &=& \frac{7.18×82.7-5.6×94.47}{5×7.18-(5.6)^2} \\[5pt] &=& 14.3 \end{eqnarray}
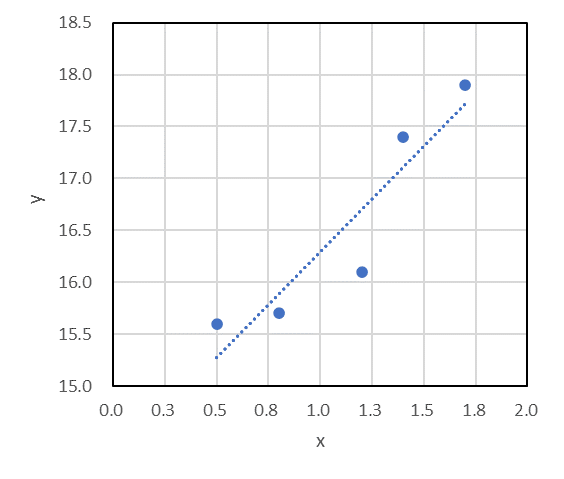
したがって最適な式 $y=2.03x + 14.3$ が得られた。
こちらもCHECK こちらもCHECK LINEST 関数を使った最小二乗法 Excelには、最小二乗法による直線式を求める関数として「LINEST 関 ... 続きを見る
最小二乗法 Excel版【関数による求め方、散布図への近似曲線と数式の表示】